1. 로지스틱 회귀 (Logistic Regression)
1.1 분류? 회귀? 악성 종양을 찾는 문제
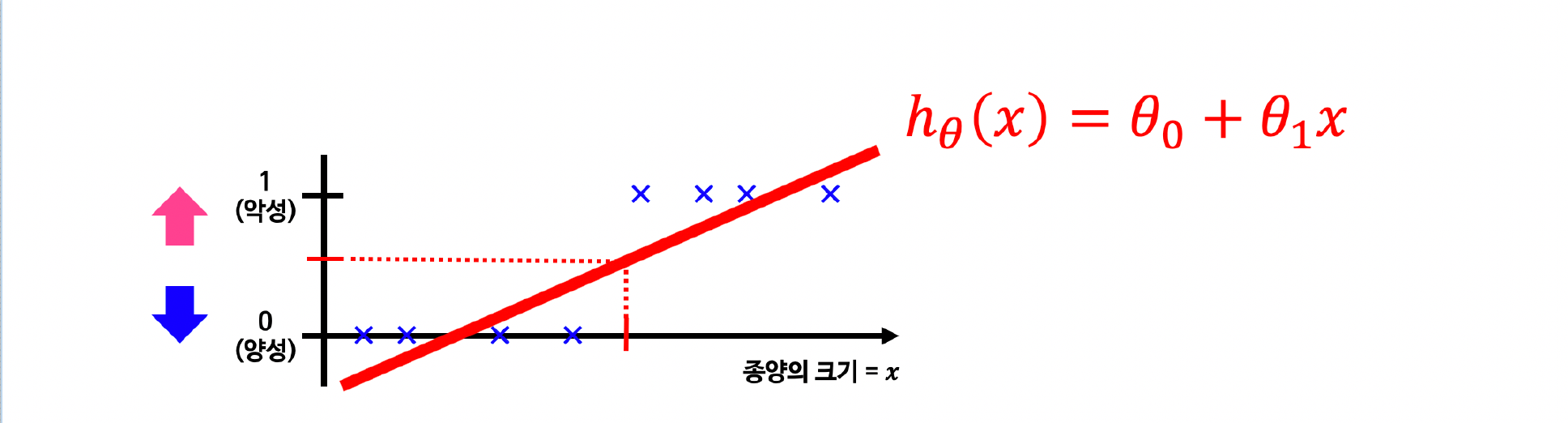
- 0.5보다 크거나 같으면 1(악성)으로 예측
- 0.5보다 작으면 0(양성)으로 예측
1.2 Linear Regression을 분류 문제에 적용?

- 회귀는 0보다 작은수, 1보다 큰수가 나오므로 그대로 분류문제에 사용할수 없음
1.3 모델 재 설정
- 분류 문제는 0 또는 1로 예측해야 하나 Linear Regression을 그대로 적용하면 예측값은 0보다 작거나 1보다 큰 값을 가지게 됨
- 예측값이 항상 0에서 1 사이의 값을 가지게 하도록 hypothesis 함수를 수정한다
1.4 Logistic Function 그래프로 보기
1
2
3
4
5
6
7
8
import numpy as np
import matplotlib.pyplot as plt
z = np.arange(-10, 10, 0.01)
g = 1 / (1 + np.exp(-z))
plt.plot(z, g)
plt.show()
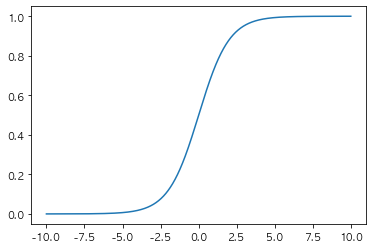
1.5 디테일하게
1
2
3
4
5
6
7
8
9
10
11
plt.figure(figsize=(12, 8))
ax = plt.gca()
ax.plot(z, g)
ax.spines['left'].set_position('zero')
ax.spines['right'].set_color('none')
ax.spines['bottom'].set_position('center')
ax.spines['top'].set_color('none')
plt.grid()
plt.show()

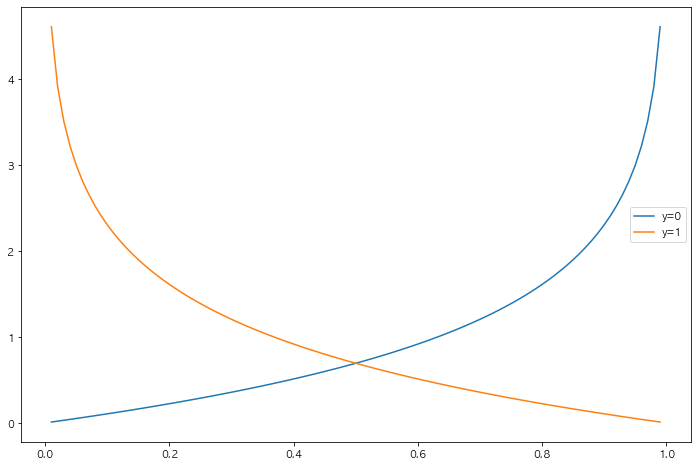
1.6 Logistic Reg, Cost Function의 그래프
1
2
3
4
5
6
7
8
9
10
11
h = np.arange(0.01, 1, 0.01)
C0 = -np.log(1 -h)
C1 = -np.log(h)
plt.figure(figsize=(12,8))
plt.plot(h, C0, label = 'y=0')
plt.plot(h, C1, label = 'y=1')
plt.legend()
plt.show()
2. Wine 데이터로 실습
2.1 데이터 로드
1
2
3
4
5
6
import pandas as pd
wine_url = 'https://raw.githubusercontent.com/hmkim312/datas/main/wine/wine.csv'
wine = pd.read_csv(wine_url, index_col=0)
wine.head()
| fixed acidity | volatile acidity | citric acid | residual sugar | chlorides | free sulfur dioxide | total sulfur dioxide | density | pH | sulphates | alcohol | quality | color | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 7.4 | 0.70 | 0.00 | 1.9 | 0.076 | 11.0 | 34.0 | 0.9978 | 3.51 | 0.56 | 9.4 | 5 | 1 |
| 1 | 7.8 | 0.88 | 0.00 | 2.6 | 0.098 | 25.0 | 67.0 | 0.9968 | 3.20 | 0.68 | 9.8 | 5 | 1 |
| 2 | 7.8 | 0.76 | 0.04 | 2.3 | 0.092 | 15.0 | 54.0 | 0.9970 | 3.26 | 0.65 | 9.8 | 5 | 1 |
| 3 | 11.2 | 0.28 | 0.56 | 1.9 | 0.075 | 17.0 | 60.0 | 0.9980 | 3.16 | 0.58 | 9.8 | 6 | 1 |
| 4 | 7.4 | 0.70 | 0.00 | 1.9 | 0.076 | 11.0 | 34.0 | 0.9978 | 3.51 | 0.56 | 9.4 | 5 | 1 |
- 실습용 자료를 git에 올려놓았음
2.2 맛등급 넣기
1
2
3
4
wine['taste']= [1. if grade > 5 else 0. for grade in wine['quality']]
X = wine.drop(['taste', 'quality'], axis = 1)
y = wine['taste']
- quality가 0보다 작으면 0, 크면 1로 하는 taste라는 컬럼을 생성
2.3 데이터 분리
1
2
3
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2, random_state = 13)
2.4 로지스틱 회귀 (LogisticRegression)
1
2
3
4
5
6
7
8
9
10
11
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score
lr = LogisticRegression(solver= 'liblinear', random_state=13)
lr.fit(X_train, y_train)
y_pred_tr = lr.predict(X_train)
y_pred_test = lr.predict(X_test)
print('Train Acc : ', accuracy_score(y_train, y_pred_tr))
print('Test Acc : ', accuracy_score(y_test, y_pred_test))
1
2
Train Acc : 0.7427361939580527
Test Acc : 0.7438461538461538
- 로지스틱 회귀 적용
- penalty : 패널티를 부여할 때 사용할 기준을 결정
- dual : bool type, dual formulation or primal formulation
- tol : 중지 기준에 대한 허용 오차 값
- C : 규칙 강도의 역수 값
- fit_intercept : bool type, 의사 결정 기능에 상수를 추가할지 여부
- class_weight : 클래스에 대한 가중치 값
- solver : 최적화에 사용할 알고리즘 (newton-cg, lbfgs, liblinear, sag, saga)
- max_iter : solver가 수렴하게 만드는 최대 반복 값
- multi_class : ovr, multinomial
2.5 파이프라인 구축
1
2
3
4
5
6
7
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
estimators = [('scaler', StandardScaler()),
('clf', LogisticRegression(solver='liblinear', random_state=13))]
pipe = Pipeline(estimators)
- Standartscaler를 적용하여 파이프라인을 구축함
2.6 학습
1
pipe.fit(X_train, y_train)
1
2
3
Pipeline(steps=[('scaler', StandardScaler()),
('clf',
LogisticRegression(random_state=13, solver='liblinear'))])
2.7 결과 확인
1
2
3
4
5
y_pred_tr = pipe.predict(X_train)
y_pred_test = pipe.predict(X_test)
print('Train Acc : ', accuracy_score(y_train, y_pred_tr))
print('Test Acc : ', accuracy_score(y_test, y_pred_test))
1
2
Train Acc : 0.7444679622859341
Test Acc : 0.7469230769230769
- 스케일러를 적용한 결과 아주 조금 Accuracy가 올랐음
2.8 Decision Tree와의 비교
1
2
3
4
5
6
from sklearn.tree import DecisionTreeClassifier
wine_tree = DecisionTreeClassifier(max_depth= 2, random_state= 13)
wine_tree.fit(X_train, y_train)
models = {'logistic Regression' : pipe, 'Decision Tree' : wine_tree}
2.9 ROC 그래프를 이용한 모델간 비교
1
2
3
4
5
6
7
8
9
10
11
12
from sklearn.metrics import roc_curve
plt.figure(figsize=(10, 8))
plt.plot([0,1], [0,1])
for model_name, model in models.items():
pred = model.predict_proba(X_test)[:, -1]
fpr, tpr, thresholds = roc_curve(y_test, pred)
plt.plot(fpr, tpr, label = model_name)
plt.grid()
plt.legend()
plt.show()
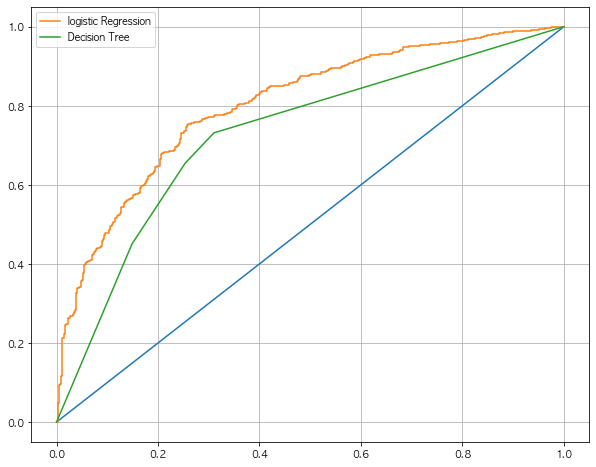
- Roc 커브를 보았을때 해당 로지스틱 회귀가 조금더 성능이 괜찮은것으로 보인다
3. PIMA 인디언 당뇨병 예측
3.1 PIMA 인디언 문제?
- 1950년대 까지 PIMA인디언은 당뇨가 없었음
- PIMA인디언은 강가 수렵을 하던 소수 인디언이나, 미국 정부에 의해 강제 이후 후 식량을 배급 받았음
- 하자만 20세기말 인구의 50%가 당뇨에 걸림
3.1 데이터 로드
1
2
3
4
5
import pandas as pd
PIMA_url = 'https://raw.githubusercontent.com/hmkim312/datas/main/pima/diabetes.csv'
PIMA = pd.read_csv(PIMA_url)
PIMA.head()
| Pregnancies | Glucose | BloodPressure | SkinThickness | Insulin | BMI | DiabetesPedigreeFunction | Age | Outcome | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 6 | 148 | 72 | 35 | 0 | 33.6 | 0.627 | 50 | 1 |
| 1 | 1 | 85 | 66 | 29 | 0 | 26.6 | 0.351 | 31 | 0 |
| 2 | 8 | 183 | 64 | 0 | 0 | 23.3 | 0.672 | 32 | 1 |
| 3 | 1 | 89 | 66 | 23 | 94 | 28.1 | 0.167 | 21 | 0 |
| 4 | 0 | 137 | 40 | 35 | 168 | 43.1 | 2.288 | 33 | 1 |
- 원본 데이터는 kaggle에 있으며, 해당 데이터를 깃헙링크를 올림
- 컬럼의 의미
- Pregnancies : 임신 횟수
- Glucose : 포도당 부하 검사 수치
- BloodPressure : 혈압
- SkinThickness : 팔 삼두근 뒤쪽의 피하지방 측정값
- Insulin : 혈청 인슐린
- BMI : 체질량 지수
- DiabetesPedigreeFunction : 당뇨 내력 가중치 값
- Age : 나이
- Outcome : 당뇨의 유무
3.2 데이터 확인
1
PIMA.info()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 768 entries, 0 to 767
Data columns (total 9 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 Pregnancies 768 non-null int64
1 Glucose 768 non-null int64
2 BloodPressure 768 non-null int64
3 SkinThickness 768 non-null int64
4 Insulin 768 non-null int64
5 BMI 768 non-null float64
6 DiabetesPedigreeFunction 768 non-null float64
7 Age 768 non-null int64
8 Outcome 768 non-null int64
dtypes: float64(2), int64(7)
memory usage: 54.1 KB
3.3 Float으로 변환
1
2
PIMA = PIMA.astype('float')
PIMA.info()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 768 entries, 0 to 767
Data columns (total 9 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 Pregnancies 768 non-null float64
1 Glucose 768 non-null float64
2 BloodPressure 768 non-null float64
3 SkinThickness 768 non-null float64
4 Insulin 768 non-null float64
5 BMI 768 non-null float64
6 DiabetesPedigreeFunction 768 non-null float64
7 Age 768 non-null float64
8 Outcome 768 non-null float64
dtypes: float64(9)
memory usage: 54.1 KB
3.4 상관관계 확인
1
2
3
4
5
6
import seaborn as sns
import matplotlib.pyplot as plt
plt.figure(figsize=(12, 10))
sns.heatmap(PIMA.corr(), cmap= 'YlGnBu')
plt.show()

- Outcome과 비교하여 상관 관계가 낮은 컬럼들이 있음
3.5 데이터가 0인 outlier가 있음
1
(PIMA == 0).astype('int').sum()
1
2
3
4
5
6
7
8
9
10
Pregnancies 111
Glucose 5
BloodPressure 35
SkinThickness 227
Insulin 374
BMI 11
DiabetesPedigreeFunction 0
Age 0
Outcome 500
dtype: int64
- 0이라는 숫자가 혈압에 있다면 문제가 있는것으로 파악
3.6 0을 평균값으로 대체
1
2
3
zero_features = ['Glucose', 'BloodPressure', 'SkinThickness', 'BMI']
PIMA[zero_features] = PIMA[zero_features].replace(0, PIMA[zero_features].mean())
(PIMA ==0).astype('int').sum()
1
2
3
4
5
6
7
8
9
10
Pregnancies 111
Glucose 0
BloodPressure 0
SkinThickness 0
Insulin 374
BMI 0
DiabetesPedigreeFunction 0
Age 0
Outcome 500
dtype: int64
- 의학적인 지삭과 PIMA 인디언에 대한 정보는 없지만, 일단 0을 평균값으로 대체함
3.7 데이터 분리
1
2
3
4
5
6
7
from sklearn.model_selection import train_test_split
X = PIMA.drop(['Outcome'], axis=1)
y = PIMA['Outcome']
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.2, random_state=13, stratify=y)
3.8 pipeline 만들기
1
2
3
4
5
6
7
8
9
10
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegression
estimators = [('scaler', StandardScaler()),
('clf', LogisticRegression(solver='liblinear', random_state=13))]
pipe_lr = Pipeline(estimators)
pipe_lr.fit(X_train, y_train)
pred = pipe_lr.predict(X_test)
- 로지스틱회귀와, 스탠다드 스케일러를 적용한 파이프라인을 구축함
3.9 수치 확인
1
2
3
4
5
6
7
from sklearn.metrics import (accuracy_score, recall_score, f1_score, precision_score, roc_auc_score)
print('Accuracy : ', accuracy_score(y_test, pred))
print('Reacll : ', recall_score(y_test, pred))
print('Precision : ', precision_score(y_test, pred))
print('AUC score: ', roc_auc_score(y_test, pred))
print('f1 score : ', f1_score(y_test, pred))
1
2
3
4
5
Accuracy : 0.7727272727272727
Reacll : 0.6111111111111112
Precision : 0.7021276595744681
AUC score: 0.7355555555555556
f1 score : 0.6534653465346535
- 사실상 해당 수치가 상대적 의미를 가질수 없어서, 이 수치 자체를 평가 할 수 없음
3.10 다변수 방정식의 각 계수값을 확인 가능
1
2
3
coeff = list(pipe_lr['clf'].coef_[0])
labels = list(X_train.columns)
coeff
1
2
3
4
5
6
7
8
[0.3542658884412649,
1.201424442503758,
-0.15840135536286715,
0.033946577129299486,
-0.16286471953988116,
0.6204045219895111,
0.3666935579557874,
0.17195965447035108]
3.11 중요한 feature그리기
1
2
3
4
5
6
7
8
features = pd.DataFrame({'Features': labels, 'importance': coeff})
features.sort_values(by=['importance'], ascending=True, inplace=True)
features['positive'] = features['importance'] > 0
features.set_index('Features', inplace=True)
features['importance'].plot(kind='barh', figsize=(
11, 6), color=features['positive'].map({True: 'blue', False: 'red'}))
plt.xlabel('Importance')
plt.show()
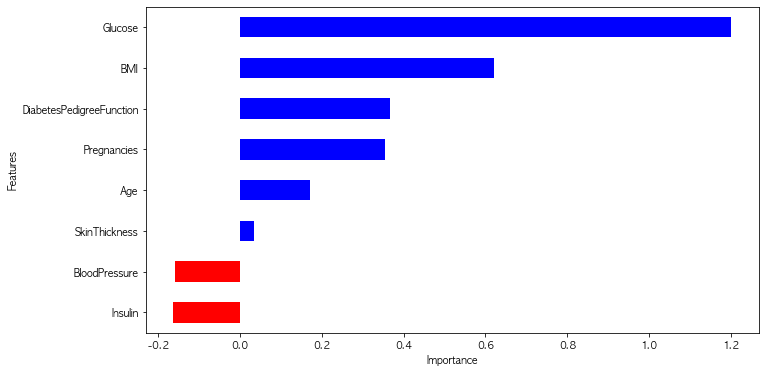
- 포도당, BMI 등은 당뇨에 영향을 미치는 정도가 높다
- 혈압은 예측에 부정적 영향을 준다
- 연령이 BMI보다 출력 변수와 더 관련되어 있었지만, 모델은 BMI와 Glucose에 더 의존한다,